数理モデルの作り方

　　・数理モデルの作り方

　　・数理モデルの作り方～実践編～

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 3話

ナユミ

科学者の人たちって本当に色々なモデルを発表してるわよね。ああいうのはどうして思いつくのかしら？

カヤ

それはまあ、天才的な直観に基づくものや、偶然の発見などもあるだろうが、地道な努力の積み重ねというところも大きいと思うぞ。

ナユミ

地道な努力かあ…。私も頑張って努力すれば、同じようなことができるのかしら？

カヤ

そうだなあ。じゃあ、数理モデルの作り方について少し勉強してみるかな。

ナユミ

うん、よろしく！

数理モデルの作り方

カヤ

さっそくだが、数理モデルの作り方の流れは次のような感じになっているんだ。

David Burghes／Morag Borrie　著、垣田高夫／大町久佐栄　訳、微分方程式で数学モデルを作ろう、2ページ目参考

　上記の著書では、数理モデルの作り方を7つのステップに分解して説明しています。

　最初のステップは現実から問題を切り出すことです。このとき、できる限り具体的に問題を言語化しておくことで、次のステップがスムーズに進められます。

　第2ステップは仮説を立てることです。仮説の立て方は様々ですが、基本的には
・調べたいことと関係していることは何か？
・どのような関係性なのか？
といった点を中心に仮説を立てるとよいです。

　第3ステップは仮説を表現する数理モデルを作ることです。このステップは他の数理モデル等を参考にしながら、仮説の数学的表現を作ります。多くの場合、仮説を表現するための数学的手法はすでに存在していますが、場合によっては新しい数学的手法を作ることも必要になります。

　第4ステップは作った数理モデルを解くことです。解き方は手計算、数値積分、あるいはもっと複雑なアルゴリズムなど様々です。

　第5ステップは得られた解を解釈することです。変数どうしの関係性はどうなっているか、ある変数が増えたときに別の変数は増えるのか減るのか、パラメータの値に応じて解はどのように変化するかなどを調べて、それが現実の問題において何を意味しているのかまで考える必要があります。

　第6ステップはモデルの評価と検討です。現実と数理モデルが適切に対応しているか判断します。両者の間に無視できない乖離が見られる場合、モデルを部分的に修正するか、場合によっては仮説を立てる段階まで戻って作り直すことも必要になります。

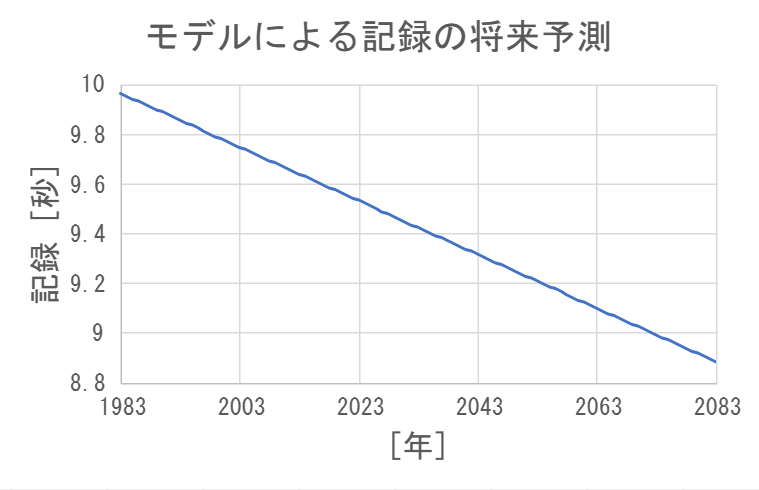
　第7ステップはモデルを使って現実の問題の説明をしたり、将来を予測したり、モデルの結果に基づいて計画を立てたりすることで、これが最終目的になります。

　以上の7ステップが数理モデルの作り方ですが、別にこの順番通りに進まなくてはいけないというものではなく、慣れてきたら各ステップを必要に応じて自由に行き来して構いません。

カヤ

余談だが、学校教育の数学は上の第4ステップばかりをやっているんだ。

ナユミ

そう言われてみれば、方程式の解き方はたくさん教えられたけど、それが現実の問題の表現に使えるみたいな話はあんまり学校では聞かなかったかも？

カヤ

だろう？受験数学は難解パズルにしないと点数に差が付かなくて試験にならない、だから学校教育の内容も難解パズルの解き方に偏ってしまうという事情はわかる。けど、もう少し現実の問題と数学との接点を紹介してもいいと個人的には思うんだな。

ナユミ

そうね。理科の時間以外にも数学の現実への応用を教える時間が増えるといいわね。

カヤ

そんな気持ちだな。それじゃあ、今までの話を非常に簡単な例を挙げて具体的にやってみよう。

数理モデルの作り方～実践編～

ナユミ

実践編…、具体的に何を調べるのかしら？

カヤ

今回は、「人類が100mを8秒台で走るのはいつか」ということについて予測したいとして、次の仮説を採用しよう。

\[ 男子 \ 100 \rm m \ 競走の世界記録は時間に比例して縮まっている\]

　単純すぎる仮説ですが、「現象が時間に比例して変化する」というこの見方はモデル化の第一歩です。この仮説を元に立てた数理モデルが次の式です。

\[ R(t) = at + b \] \( R \) は記録 [秒]、\( t \) は時刻 [年]、\( a \) 、\( b \) は定数。

　記録は時間の関数で、比例の関係、つまり直線の式になっています。今回はここまで簡単なモデルにしたので、これがそのままモデルの解と呼べます。

ナユミ

解く手間がなかったわね。

カヤ

歯ごたえがなかったかもしれないが、まあ簡単な例を選んだ結果だから許してくれ。このモデルからわかることは、当たり前だが、記録 \( R \) が時刻 \( t \) に比例して変化するということだ。

ナユミ

そうね。記録は縮まっていくだろうから、定数 \( a \) は負の値になりそうね。

カヤ

まあそうだろうな。とまあ、大体モデルの解のふるまいはわかったので、さっそくこのモデルが実際の世界記録に合致するか調べてみたらこうなった。

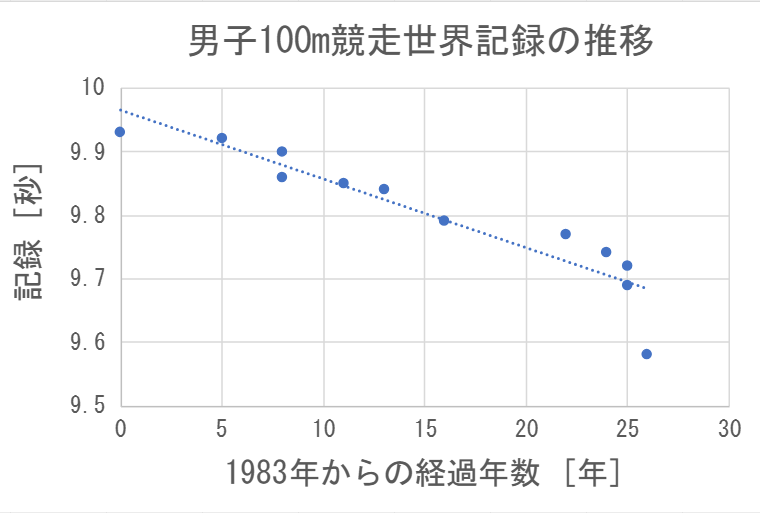
グラフ中に青丸で示した記録は「Wikipedia　男子100メートル競走世界記録の推移」より。

　グラフに書かれた破線がモデルです。パラメータの数値を書くと次式になります。

\[ R(t) = -0.0108t + 9.9633 \]

　\( a \) の値から一年あたりおよそ \( 0.0108 \) 秒のペースで記録が更新されているとわかります。最後の点だけ直線に乗っていませんが、この点は2009年の世界陸上ベルリン大会でウサイン・ボルトが樹立した9秒58という記録です。ボルトはちょうどこの一年前に北京オリンピックで9秒69の世界記録を樹立しています。つまり、1年間で0.11秒も記録を更新しており、これは平均的なペースの10倍の速さでの記録更新です。

カヤ

やっぱりボルトはすごかったんだな。

ナユミ

そうね。そういえば、このグラフ、始まりが1983年ってことになってるけど、これより前の記録はないの？

カヤ

ああ、それは1983年より前の記録もあるにはあるんだが、手動の計測も混ざってたから、計測が電動に変わってからのデータで手に入ったものを使っているんだ。

ナユミ

昔は計測も手作業だったのね。

カヤ

3人がかりで測定していたらしいぞ。

ナユミ

時代を感じるわ…。

カヤ

だな。それで、このモデルを使って1983年から100年後の2083年までの記録の推移を予測してみたものがこのグラフだ。

ナユミ

9秒台切ってるわね。

カヤ

ああ。このグラフでいくと、2073年には9秒台を切ることが予想される。あと50年後だから、カヤもまだ生きてるかな。

ナユミ

生きてる間に見れるといいわね。

カヤ

ああ、頑張って健康維持しよう。

ナユミ

今日は数理モデルの作り方が知れてよかったわ。ありがと!

カヤ

どういたしまして。数理モデルは自分で作ったり、様々な具体例を知ることでより理解が深まるから、「数値実験」の他の記事もぜひ見てくれよな。

参考：
[1] David Burghes／Morag Borrie　著、垣田高夫／大町久佐栄　訳、微分方程式で数学モデルを作ろう、日本評論社、1990年4月28日発行
[2] Wikipedia　男子100メートル競走世界記録の推移、https://ja.wikipedia.org/wiki/男子100メートル競走世界記録の推移、2023年8月4日閲覧

三角関数おみくじ