TABLE OF CONTENTS
・Increase/Decrease and Extrema of Functions
Kaya
This time, let’s go over the increase/decrease and extrema of functions of one variable.
Increase/Decrease and Extrema of Functions
Nayumi
A function increases and decreases, doesn’t it?
Kaya
Exactly. That increase and decrease can be characterized in the following way using the derivative.
Let \( y = f(x) \) be a differentiable function on a real interval containing \( a \). Then,
\[ f'(a) \gt 0 \ \ \Rightarrow \ \ f(x) \text{ is increasing at } x = a, \]
\[ f'(a) \lt 0 \ \ \Rightarrow \ \ f(x) \text{ is decreasing at } x = a. \]
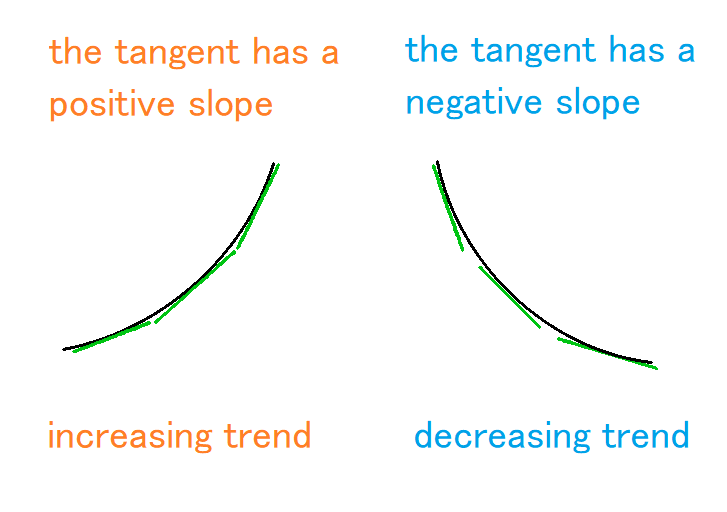
The derivative of a function of one variable is the slope of the tangent.
In other words, the above statement means that if the slope of the tangent is positive, then the function is
increasing; conversely, if the slope of the tangent is negative, then the function is decreasing.
This can be illustrated as follows.
Nayumi
If the tangent slopes upward to the right, the function is increasing; conversely, if it slopes downward
to the right, the function is decreasing. Looking at the figure, it seems obvious.
Kaya
Exactly. Now, let’s move on to the explanation of extrema.
\[ \text{Extrema}\]
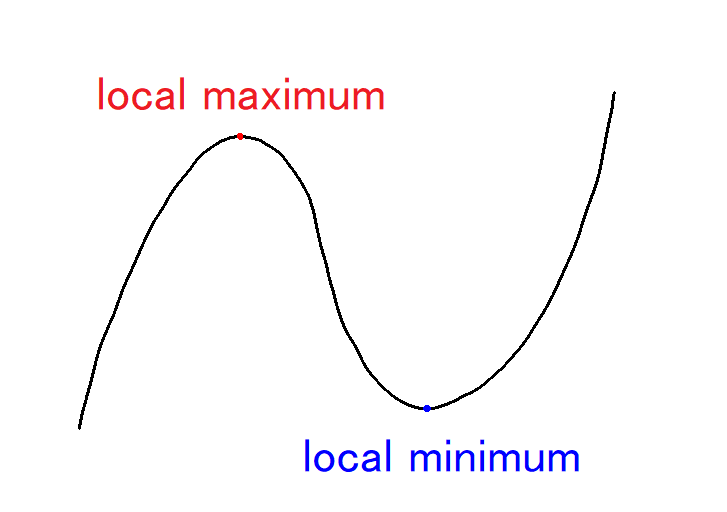
When the function of one variable \( y = f(x) \) turns from an increasing trend to a decreasing trend
at the boundary of \( x = a \), \( f(a) \) is called a local maximum.
On the other hand, when the function of one variable \( y = f(x) \) turns from an decreasing trend to a increasing trend at the boundary of \( x = a \), \( f(a) \) is called a local minimum.
Each of a local maximum and a local minimum is called an extremum; together, they are called extrema.
On the other hand, when the function of one variable \( y = f(x) \) turns from an decreasing trend to a increasing trend at the boundary of \( x = a \), \( f(a) \) is called a local minimum.
Each of a local maximum and a local minimum is called an extremum; together, they are called extrema.
Nayumi
It’s more like a ridge and the bottom of a valley than a mountain peak.
Kaya
Exactly. A local maximum is different from a global maximum, so thinking of it as a ridge rather than a
mountain peak is a good metaphor.
Nayumi
This “mountain” still seems climbable toward the right side of the valley.
Kaya
Right. And the following holds for extrema.
Suppose that function of one variable \( y = f(x) \) is differentiable on the real interval containing
\( a \).
In this case, if \( y = f(x) \) takes the extremum on \( x = a \), then \( f'(a) = 0 \).
At an extremum, increase and decrease switch over; that is, the value of the derivative changes from
positive to negative (or vice versa). At such a switching point, we have \( f'(a) = 0 \).
Using this property, we can determine the \( x \)-values at which the graph of a function has a ridge or a valley, and also investigate whether the function as a whole has such ridges or valleys.
Using this property, we can determine the \( x \)-values at which the graph of a function has a ridge or a valley, and also investigate whether the function as a whole has such ridges or valleys.
Nayumi
That seems pretty useful in many ways.
Kaya
Yeah. You’ll probably need it later, so make sure to remember it.
Nayumi
Alright.
References：
[1] 石村園子, やさしく学べる微分積分, 共立出版, December 25, 1999
Previous
Ep. 9
Euler method
Euler method
Next
Ep. 11
Partial fraction decomposition
Partial fraction decomposition