TABLE OF CONTENTS
・Partial fraction decomposition
Kaya
This time, let’s go over partial fraction decomposition.
Partial fraction decomposition
Partial fraction decomposition is the operation of splitting a fraction into two parts.
Let’s start with the basic form and consider the following decomposition.
We’re looking for \( k \) that satisfies
\[ \frac{1}{ab} = k \left( \frac{1}{a} + \frac{1}{b} \right). \]
Nayumi
Hm, I think we can figure this out if we find a common denominator inside the parentheses on the
right-hand side.
\[ \begin{align}
\frac{1}{ab} &= k \left( \frac{1}{a} + \frac{1}{b} \right) \\\\
\frac{1}{ab} &= k \left( \frac{a+b}{ab} \right)
\end{align}\]
Compare both sides,
\[ 1 = k \left( a+b \right) \]
Thus,
\[ k = \frac{1}{a+b} \]
Kaya
Correct. From this result, we can see that the following equation holds.
\[ \frac{1}{ab} = \frac{1}{a+b} \left( \frac{1}{a} + \frac{1}{b} \right) = \frac{1}{a \left( a + b
\right) } + \frac{1}{b \left( a + b \right)} \]
Nayumi
The expression on the far right was expanded again inside the parentheses, wasn’t it?
Kaya
That’s right. Each fraction in that rightmost expression can be further decomposed by applying the same
formula again.
\[ \begin{align}
\frac{1}{a \left( a + b \right) } &= \frac{1}{a + \left( a + b \right)} \left( \frac{1}{a} +
\frac{1}{a+b} \right) \\\\
&= \frac{1}{2a+b} \left( \frac{1}{a} + \frac{1}{a+b} \right) \\\\
\frac{1}{b \left( a + b \right)} &= \frac{1}{b + \left( a + b \right)} \left( \frac{1}{b} +
\frac{1}{a+b} \right) \\\\
&= \frac{1}{a + 2b} \left( \frac{1}{b} + \frac{1}{a+b} \right)
\end{align}\]
Nayumi
I see, in the upper equation you’re using the formula with \( a = a \) and \( b = a + b \), while in the
lower one you’re using \( a = b \) and \( b = a + b \).
Using the same formula inside itself — that’s kind of matryoshka-like.
Kaya
Exactly. By taking advantage of this property that lets us repeat the decomposition, we can do things
like this, for example.
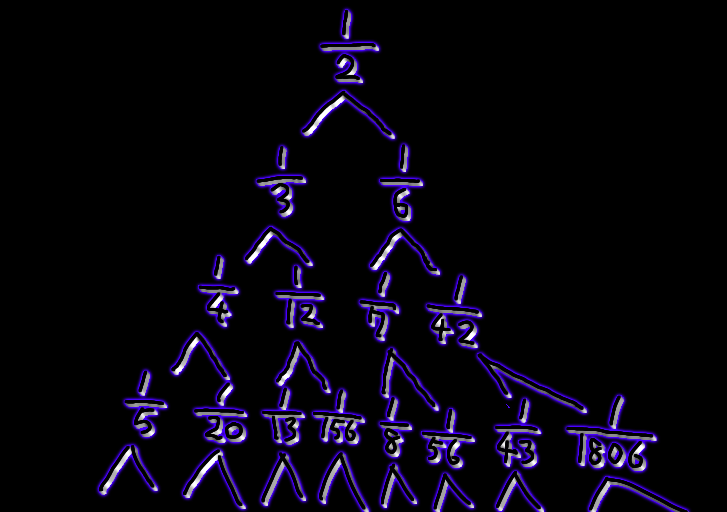
\[ \begin{align}
\frac{1}{2} &= \frac{1}{1 \cdot 3} + \frac{1}{2 \cdot 3} \\\\
&= \frac{1}{1 \cdot 4} + \frac{1}{3 \cdot 4} + \frac{1}{2 \cdot 5} + \frac{1}{3 \cdot 5} \\\\
&= \frac{1}{1 \cdot 5} + \frac{1}{4 \cdot 5} + \frac{1}{3 \cdot 7} + \frac{1}{4 \cdot 7} + \frac{1}{2
\cdot 7} + \frac{1}{5 \cdot 7} + \frac{1}{3 \cdot 8} + \frac{1}{5 \cdot 8} \\\\
&= \ldots
\end{align}\]
Nayumi
You can keep decomposing it endlessly, huh? My head’s starting to spin…
Kaya
Well, this was just for fun, so don’t worry too much about it.
Nayumi
I’ll just let that one slide.
Kaya
Please do. Now then, let’s take a look at the next problem.
We’re looking for \( p \) and \( q \) that satisfy
\[ \frac{1}{\left( ax+b \right) \left( cx+d \right)} = \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \]
Nayumi
I feel like I’ve seen this form a few times before…
Kaya
I bet you have. We’ve run into expressions like the one on the left before — we’d rewrite them into the
form on the right and then take the indefinite integral.
Nayumi
Looks like we just need to find a common denominator on the right-hand side for this one too.
\[ \begin{align}
\frac{1}{\left( ax+b \right) \left( cx+d \right)} &= \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \\\\
&= \frac{p \left( cx+d \right) + q \left( ax+b \right)}{\left( ax+b \right) \left( cx+d \right)} \\\\
&= \frac{\left( cp + aq \right) x + dp + bq}{\left( ax+b \right) \left( cx+d \right)}
\end{align}\]
Nayumi
Wait, what do we do from here again?
As before, we compare the left-hand side and the right-hand side.
However, this time we want to find \( p \) and \( q \), so we need to set up two equations involving these
variables.
Meanwhile, \( x \) also appears in the denominators. If we were to express it in terms of the other symbols in the denominators, such as \( a \) or \( b \), it would effectively change the denominators themselves — which would be inconvenient.
Therefore, we handle this by setting the coefficient of \( x \) in the numerator equal to 0, and the part independent of \( x \) equal to 1.
Meanwhile, \( x \) also appears in the denominators. If we were to express it in terms of the other symbols in the denominators, such as \( a \) or \( b \), it would effectively change the denominators themselves — which would be inconvenient.
Therefore, we handle this by setting the coefficient of \( x \) in the numerator equal to 0, and the part independent of \( x \) equal to 1.
\[ \begin{align}
[1] \ \ \ \ cp + aq &= 0 \\\\
[2] \ \ \ \ dp + bq &= 1
\end{align}\]
Nayumi
I see, doing that lets us neatly set up two equations for \( p \) and \( q \).
Kaya
Exactly. We can solve it as follows.
From [1], we have
\[ q = - \frac{c}{a} p \]
Substituting this into [2], we get
\[ \begin{align}
dp - \frac{bc}{a} p &= 1 \\\\
p \left( d - \frac{bc}{a} \right) &= 1 \\\\
p \cdot \frac{ad - bc}{a} &= 1 \\\\
p &= \frac{a}{ad - bc}
\end{align}\]
Therefore,
\[ \begin{align}
q &= - \frac{c}{a} p \\\\
&= - \frac{c}{a} \cdot \frac{a}{ad - bc} \\\\
&= - \frac{c}{ad - bc}
\end{align}\]
Nayumi
So you rearranged [1] to express \( q \) in terms of \( p \), substituted that into [2] to find \( p \),
and then plugged it back into [1] to get \( q \).
Kaya
Exactly. When we substitute these back into the original equation, we get the following.
\[ \begin{align}
\frac{1}{\left( ax+b \right) \left( cx+d \right)} &= \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \\\\
&= \left( \frac{\frac{a}{ad - bc}}{ax+b} + \frac{- \frac{c}{ad - bc}}{cx+d} \right) \\\\
&= \frac{1}{ad - bc} \left( \frac{a}{ax+b} - \frac{c}{cx+d} \right)
\end{align}\]
Nayumi
So this is the formula you often uses, right?
Kaya
That’s right. You might see it again from time to time, so keep it in mind.
Nayumi
Got it.
References：
[1] Partial fraction decomposition, https://en.wikipedia.org/wiki/Partial_fraction_decomposition,
October 20, 2025
Previous
Ep. 10
Increase/Decrease
and extrema
Increase/Decrease
and extrema