
TABLE OF CONTENTS
・How to build a mathematical model
・How to build a mathematical model: practical edition
How to build a mathematical model
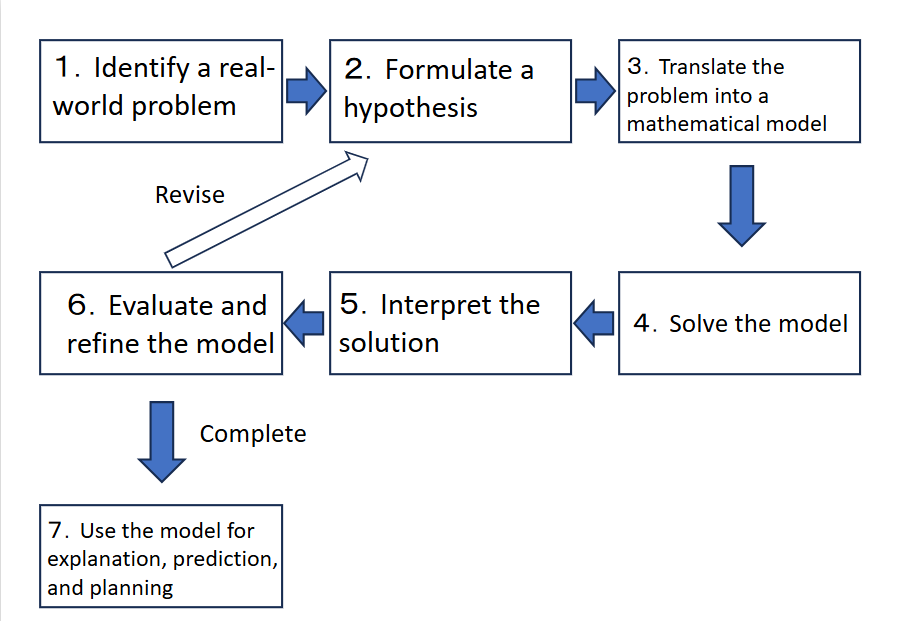
The process of constructing a mathematical model is broken down into seven steps.
The first step is to extract a problem from reality. At this stage, it is important to describe the problem as concretely and clearly as possible in words—this makes it easier to proceed to the next step.
The second step is to formulate a hypothesis. There are many ways to do this, but a good starting point is to ask:
・What factors are related to what I want to investigate?
・How are those factors related?
Focusing on these questions can help build a solid hypothesis.
The third step is to construct a mathematical model that represents the hypothesis. This step involves expressing the hypothesis in mathematical terms, often by referring to existing models and methods. In many cases, the mathematical tools needed already exist, but in some cases, it may be necessary to develop new ones.
The fourth step is to solve the mathematical model. Methods for doing this may include analytical techniques, numerical integration, or more complex algorithms, depending on the situation.
The fifth step is to interpret the solution. You need to investigate things like:
— How are the variables related?
— When one variable increases, does another increase or decrease?
— How does the solution change depending on parameter values?
Ultimately, you must consider what these mathematical results mean in the context of the real-world problem.
The sixth step is to evaluate and refine the model. You check whether the model appropriately reflects reality. If there are significant discrepancies between the model and actual observations, you may need to revise parts of the model—or even return to the hypothesis stage and start over.
The seventh and final step is to apply the model—to explain real-world phenomena, make predictions about the future, or design strategies based on the model’s outcomes. This is the ultimate purpose of constructing a mathematical model.
These seven steps outline the general process of building a mathematical model. However, it’s not necessary to follow them in strict order. Once you become familiar with the process, you can move flexibly between steps as needed.
The first step is to extract a problem from reality. At this stage, it is important to describe the problem as concretely and clearly as possible in words—this makes it easier to proceed to the next step.
The second step is to formulate a hypothesis. There are many ways to do this, but a good starting point is to ask:
・What factors are related to what I want to investigate?
・How are those factors related?
Focusing on these questions can help build a solid hypothesis.
The third step is to construct a mathematical model that represents the hypothesis. This step involves expressing the hypothesis in mathematical terms, often by referring to existing models and methods. In many cases, the mathematical tools needed already exist, but in some cases, it may be necessary to develop new ones.
The fourth step is to solve the mathematical model. Methods for doing this may include analytical techniques, numerical integration, or more complex algorithms, depending on the situation.
The fifth step is to interpret the solution. You need to investigate things like:
— How are the variables related?
— When one variable increases, does another increase or decrease?
— How does the solution change depending on parameter values?
Ultimately, you must consider what these mathematical results mean in the context of the real-world problem.
The sixth step is to evaluate and refine the model. You check whether the model appropriately reflects reality. If there are significant discrepancies between the model and actual observations, you may need to revise parts of the model—or even return to the hypothesis stage and start over.
The seventh and final step is to apply the model—to explain real-world phenomena, make predictions about the future, or design strategies based on the model’s outcomes. This is the ultimate purpose of constructing a mathematical model.
These seven steps outline the general process of building a mathematical model. However, it’s not necessary to follow them in strict order. Once you become familiar with the process, you can move flexibly between steps as needed.
How to build a mathematical model: practical edition
\[ \text{The men's 100-meter WR has been decreasing in proportion to time.}\]
Although this is a very simple hypothesis, viewing a phenomenon as changing in proportion to time is a
crucial first step in modeling.
Based on this hypothesis, we arrive at the following mathematical model:
\[ R(t) = at + b \]
Here, \( R \) represents the record (in seconds), \( t \) is time (in years), and \( a \) and \( b \) are
constants.
In this model, the record is treated as a function of time, following a proportional (linear)
relationship—essentially, it's the equation of a straight line.
Since we've kept the model this simple, this equation itself can be considered the solution to the model.
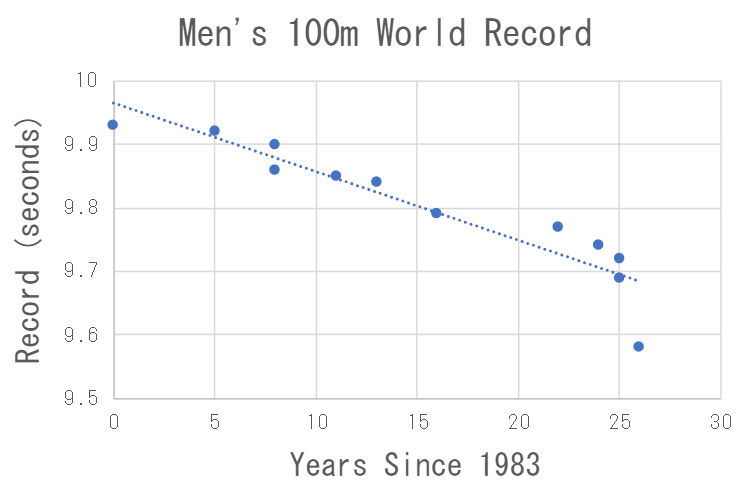
The records indicated by blue dots in the graph are taken from the Wikipedia page "Men's 100 metres world record progression."
The dashed line in the graph represents the model. With the parameter values included, the model is
expressed by the following equation.
\[ R(t) = -0.0108t + 9.9633 \]
From the value of \( a \), we can see that the world record has been improving at a pace of approximately
0.0108 seconds per year.
The final data point doesn't fall on the straight line, however. This point represents the 9.58-second world
record set by Usain Bolt at the 2009 World Championships in Berlin.
Just one year earlier, at the 2008 Beijing Olympics, Bolt had already set a world record of 9.69 seconds.
In other words, the record improved by 0.11 seconds in a single year—ten times faster than the average pace
of improvement.
References:
[1] David Burghes/Morag Borrie, Modelling with Differential Equations, Ellis Horwood Ltd, April 22, 1981
[2] Wikipedia Men's 100 metres world record progression,https://en.wikipedia.org/wiki/Men%27s_100_metres_world_record_progression,
August 4, 2023